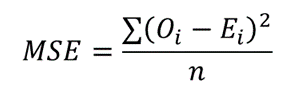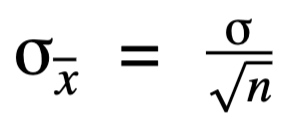Mittlerer prozentualer Fehler

Der mittlere prozentuale Fehler (MPE) ist ein Fehlermaß, das angibt, um wie viel Prozent eine Modellvorhersage ${\displaystyle f}$ im Schnitt von dem echten Wert ${\displaystyle a}$ abweicht

${\displaystyle {\text{MPE}}={\frac {100\%}{n}}\sum _{t=1}^{n}{\frac {a_{t}-f_{t}}{a_{t}}}.}$

Dabei sind die ${\displaystyle a_{t}}$ die zur Zeit oder an der Stelle ${\displaystyle t=1,\ldots n}$ vorgefundenen Werte und ${\displaystyle f_{t}}$ die entsprechenden Prognosewerte aus dem Modell.

Alternativen

• Verwandt ist der mittlere absolute prozentuale Fehler

${\displaystyle {\text{MAPE}}={\frac {100\%}{n}}\sum _{t=1}^{n}\left|{\frac {a_{t}-f_{t}}{a_{t}}}\right|.}$, welcher in der empirischen Risikominimierung auftritt.

• Mittlerer absoluter skalierter Fehler (Mean Absolute Scaled Error, MASE)
• Symmetrischer mittlerer absoluter prozentualer Fehler (Symmetric Mean Absolute Percentage Error, sMAPE)
• Mittlere Richtungsgenauigkeit (Mean Directional Accuracy, MDA)
• Mittlerer Arcustangens des absoluten prozentualen Fehlers (Mean Arctangent Absolute Percentage Error, MAAPE)
• Mittlerer quadrierter logarithmischer Fehler

Einzelnachweise